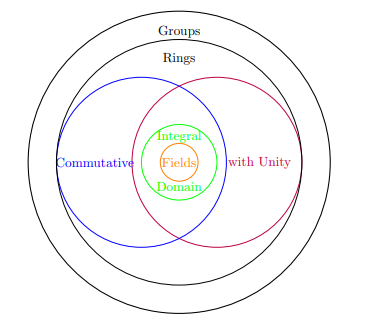
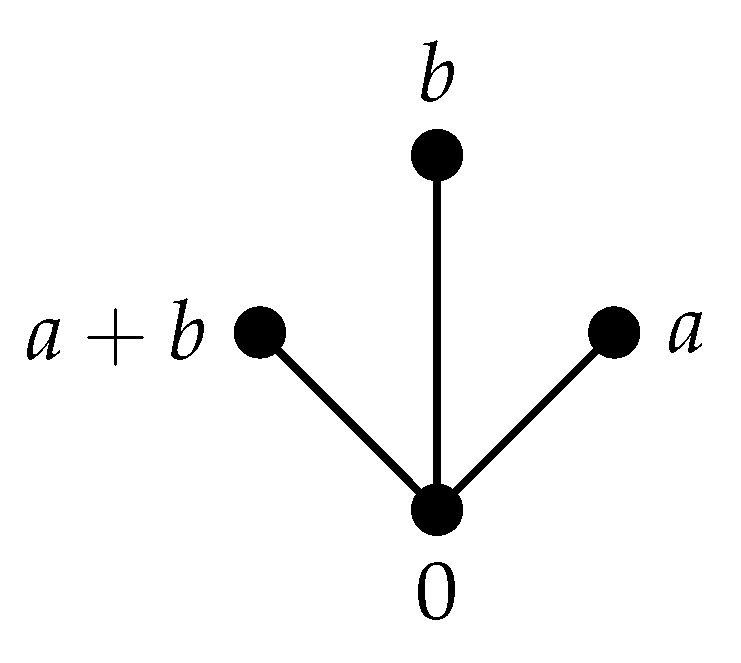abstract algebra - Prove that the set A satisfies all the axioms to be a commutative ring with unity. Indicate the zero element, the unity and the negative. - Mathematics Stack Exchange

Axioms | Free Full-Text | Unification Theories: Rings, Boolean Algebras and Yang–Baxter Systems

abstract algebra - Why is commutativity optional in multiplication for rings? - Mathematics Stack Exchange

ALISON'S AXIOMS: The Search For The Ring Of Ramanujan: Cooper, Christopher, Bronowski, Emily, Formatting, Paradox Book Covers: 9798581311493: Amazon.com: Books

SOLVED: Let R be a ring. Suppose that due to a printer error, the addition and multiplication tables for R were printed with several entries missing, as shown below: Using only the


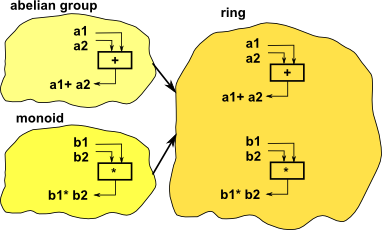
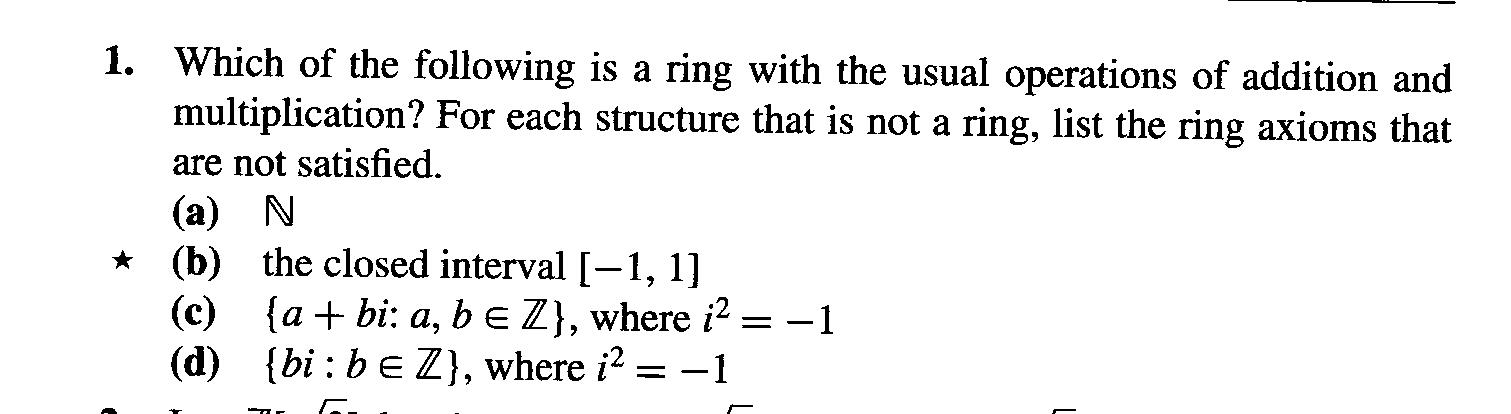









![summarizes the axioms that define groups, rings, and field[Sta05] | Download Scientific Diagram summarizes the axioms that define groups, rings, and field[Sta05] | Download Scientific Diagram](https://www.researchgate.net/publication/312277471/figure/fig1/AS:449838375542784@1484261234519/1-summarizes-the-axioms-that-define-groups-rings-and-fieldSta05.png)